Morphological image processing
Here's a cool little topic. Let's think about how to extract borders in an image. I'm sure you could think of hundreds of heuristics, but I'd like to discuss one particular heuristic that, indirectly, leads to some pretty cool results relating to cellular automata.
The technique is called "morphology", and it's one of those ideas which starts out with very simple rules, but, when the rules are composed, can yield complex behaviour.
The central components in morphology are that of a union, complement and erosion of images. We'll only be working with pure black-and-white images here, but this can all be extended (with some effort) to grayscale and color images. If we represent images $A$ and $B$ as the set of coordinate-pairs for all black pixels, then $A\cup B$ is the normal set union, the resulting image being a "combination" of both. The complement, $A^c$, just flips black pixels to white, and white pixels to black. Here are some examples
$\cup$ $=$
and
$^c$ $=$
Erosion
Erosion, however, is an operation which takes a normal image $A$, and a so called structure element, $S$, to produce a new image $B$. A structure element is a just small mini-image, typically something like a $3\times 3$ set of black pixels. The erosion, $A\ominus S$, then, is the act of placing the center of the structure element (or some arbitrarily center-replacement if the width is even) at each pixel of the input image $A$ and asking "does this local image patch look identical to the structure element?". If the answer is yes, a black pixel is placed on that position of output image.
Formally, you could express this operation as $$ A\ominus S = \Big\{ (x,y)\ |\ S_{(x,y)}\subset A \Big\} $$ where $S_{(x,y)} = \{ (x+i,y+j)\ |\ (i,j)\in S \}$ is just the translation of $S$ to postion $(x,y)$. (Here we're using the version which translates the upper-left-corner, but I'll leave it as an exercise to express how to translate from the center.)
Here's an example:
$\ominus$ $=$
Dilation
With these basic components we could start defining higher-order operations. I'll only cover dilation, which is simply $$ A\oplus S = (A^c \ominus S)^c $$ As the name implies, this operation sort of "expands" the objects in the image
$\oplus$ $=$
Borders
We don't actually need higher-order operations to solve the original problem posed. How do you use this to extract borders? The solution is natural in this algebra of images that we've developed $$ \beta(A) = A - A\ominus S $$ where $X-Y = X\cap Y^c = (X^c\cup Y)^c $. In other words, just contract the objects in the image slightly, and then look at the difference between the original image and the result.
$\beta$ $\Bigg($ $\Bigg)$ $= $
 ,
$S_2 =$
,
$S_2 =$ ,
$S_3 =$
,
$S_3 =$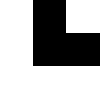 ,$\dots$,
and $S_{k+1}, \dots, S_n$ those which satisfy the second
rule.
,$\dots$,
and $S_{k+1}, \dots, S_n$ those which satisfy the second
rule.