When initializing the weight matrix (let's assume there is only one) in an RNN (recurrent neural network) it is said (e.g. by Ilya Sutskever in his PhD thesis) that you want the spectral radius (the size of the largest eigenvalue in absolute value) to be slightly less than $1$.
A common way to initialize the weight matrix is,
size = 100
variance = 0.1
W = np.random.randn(size, size)*variance
and then play with the variance until it works.
In this post we'll do a bit of exploratory mathematics to prod the how the variance and size of a matrix, $W$, affects its spectral radius $\rho(W)$.
Since the spectral radius is somewhat difficult to work with theoretically, we'll take an experimental approach instead.
Let $W_{n,v}$ be the random matrix of size $n$ consisting of (zero mean) gaussian entries with variance $v$. The spectral radius is a random variable of these entries. How does the distribution of the spectral radius look for, say, $W_{10,2}$? Sampling a set of $10,000$ matrices from this distibution gives the following result.
It looks somewhat Poisson distributed! We could stop here, conjecture that it indeed is, and then try to prove it, but let's move on.
Typically when training RNNs the number of hidden units is first decided upon, and then you go about mucking with the variance. Below I've fixed the matrix size to $10$. I then changed the variance between $0.1$ and $10$, and looked at the expected spectral radius (since all we really care about is that $E\{ \rho(W)\} \approx 1$).
It looks linear! That's nice. The coefficient here is about $3$. Thus, for the case of $n=10$, we know that if our variance is, say, $v=0.1$, then the spectral radius will be about $\rho(W_{10,0.1}) = 0.3$.
What if we train the network, and then decide that we'd really like more hidden units? Can we be sure that the spectral radius will stay the same (assuming we don't change the variance)?
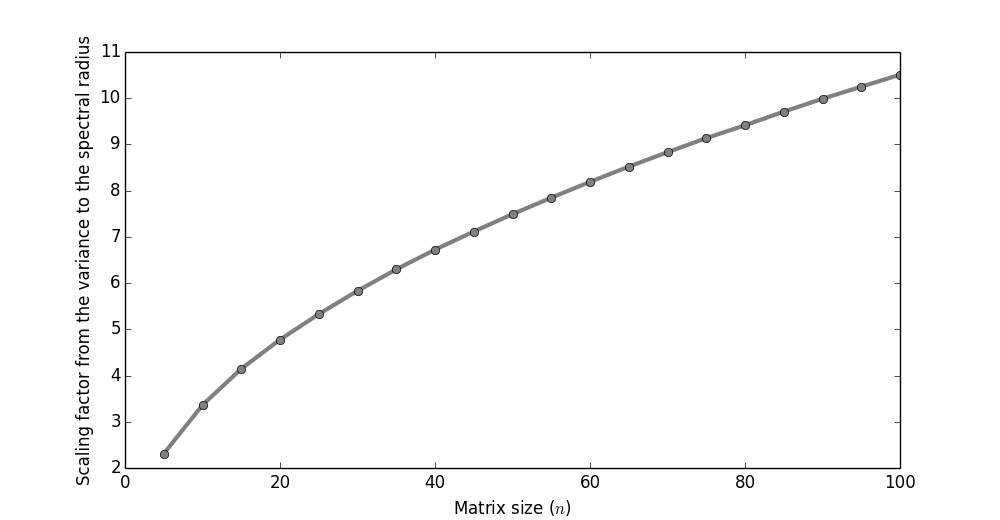
Above I'm varying the size of the matrix, while looking at the proportion between the expected spectral radius and variance in the entries. It's not constant!
In other words, be aware that when increasing the size of a matrix then its spectral radius will also increase.
The conclusion of this post is basically just that if you have something like this in your code,
size = 100
variance = 0.1
W = np.random.randn(size, size)*variance
then you should be aware that if you change the size of the matrix, then you'll also have to change the variance.
How could we go about fixing this? Preferably we'd like a theoretically motivated expression between the variance, size of the matrix, and spectral radius, so that we can ensure the radius is size-invariant (by automatically changing the variance).
Doing it theoretically is a theorem for another day. But one ad hoc method often suggested is the following. (There are theoretical arguments, but I've never seen one from the perspective of trying to keep the spectral radius fixed.)
size = 100
variance = 0.1 / np.sqrt(size)
W = np.random.randn(size, size)*variance
Amazingly, when we calculate the proportion between the expected spectral radius and the variance, as a function of the matrix size (using the normalization trick above), it's almost always at $\sim 1$.
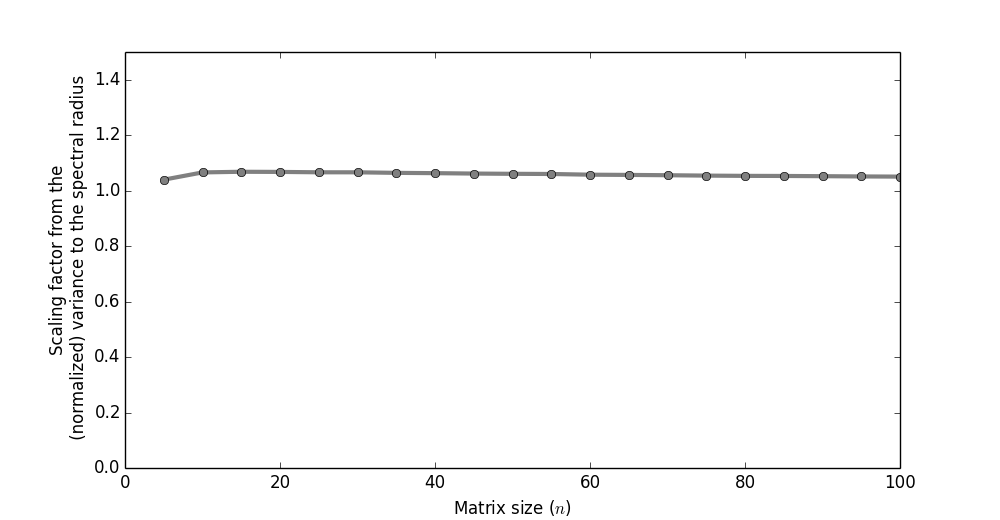
The conclusion is that when you want the spectral radius to remain fixed; just use the above instead.